Infinite-order rogue waves that are small (but not small in $L^2$)
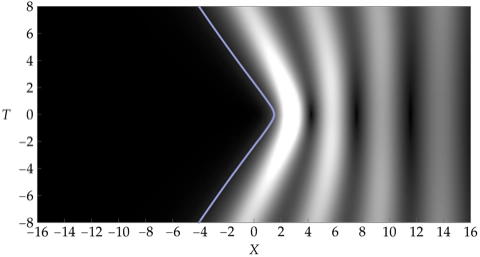 Infinite-order rogue wave in the elliptic spread asymptotic regime.
Infinite-order rogue wave in the elliptic spread asymptotic regime.
Abstract
General rogue waves of infinite order constitute a family of solutions of the focusing nonlinear Schrödinger equation that have recently been identified in a variety of asymptotic limits such as high-order iteration of Bäcklund transformations and semiclassical focusing of pulses with specific amplitude profiles. These solutions have compelling properties such as finite $L^2$-norm contrasted with anomalously slow temporal decay in the absence of coherent structures. In this paper we investigate the asymptotic behavior of general rogue waves of infinite order in a parametric limit in which the solution becomes small uniformly on compact sets while the $L^2$-norm remains fixed. We show that the solution is primarily concentrated on one side of a specific curve in logarithmically rescaled space-time coordinates, and we obtain the leading-order asymptotic behavior of the solution in this region in terms of elliptic functions as well as near the boundary curve in terms of modulated solitons. The asymptotic formula captures the fixed $L^2$-norm even as the solution becomes uniformly small.
Type
Publication
Preprint
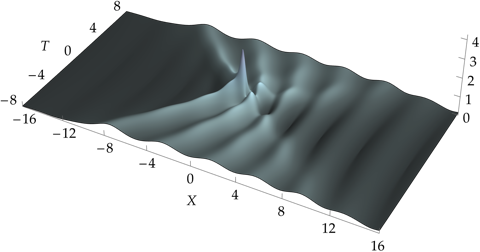
Infinite-order rogue wave in the ’elliptic spread’ asymptotic regime.
I thank the kind team at Baudry Greene on Endell Street in London for their hospitality and the excellent coffee they provided during the final stages of preparing this article.