Numerical inverse scattering for the Toda lattice
Time evolution of purely dispersive initial data is computed at $t=10000$ without time-stepping, at least by setting $t=10000$ in the Riemann-Hilbert problem and solving different Riemann-Hilbert problems as $n$ varies. Below are plots of $a_n$ (the off-diagonal of the bi-infinite Jacobi matrix) and $b_n$ (the diagonal of the bi-infinite Jacobi matrix).
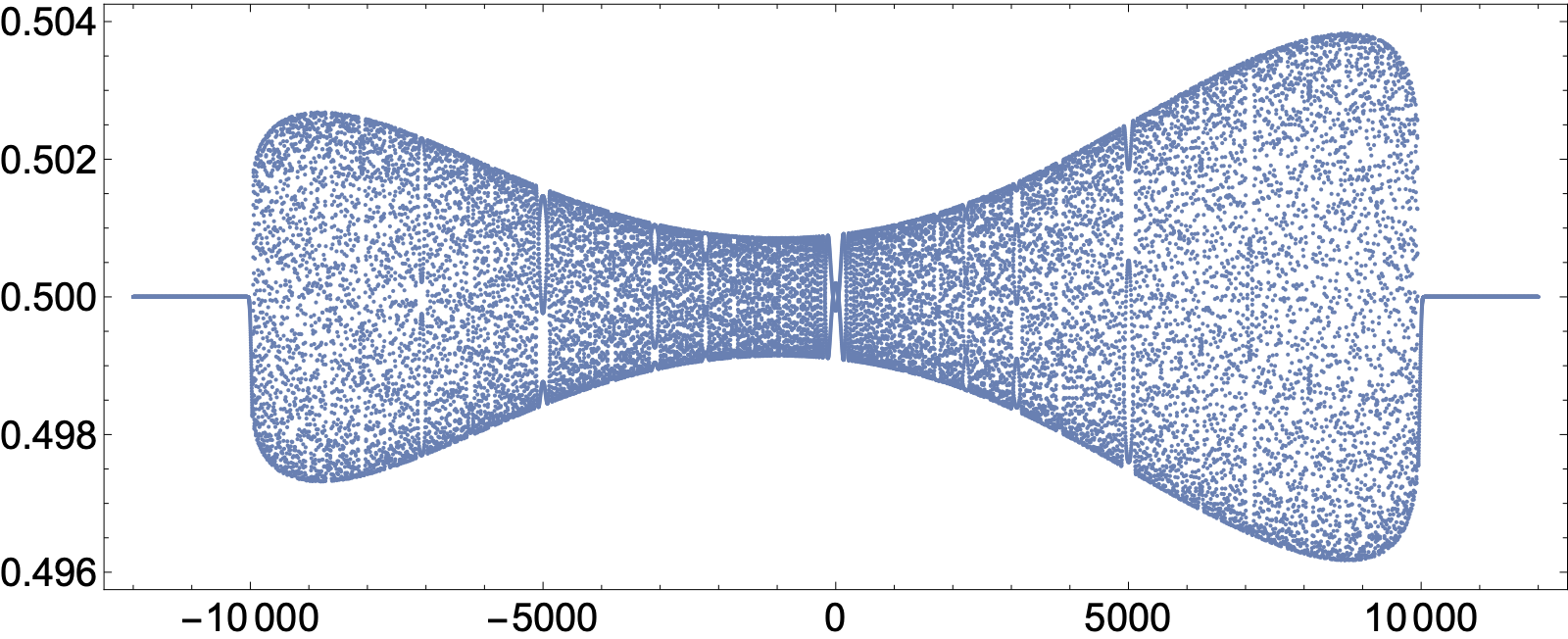
$a_n(t=10000)$, $-7500\leq n\leq 7500$. There are no solitons.
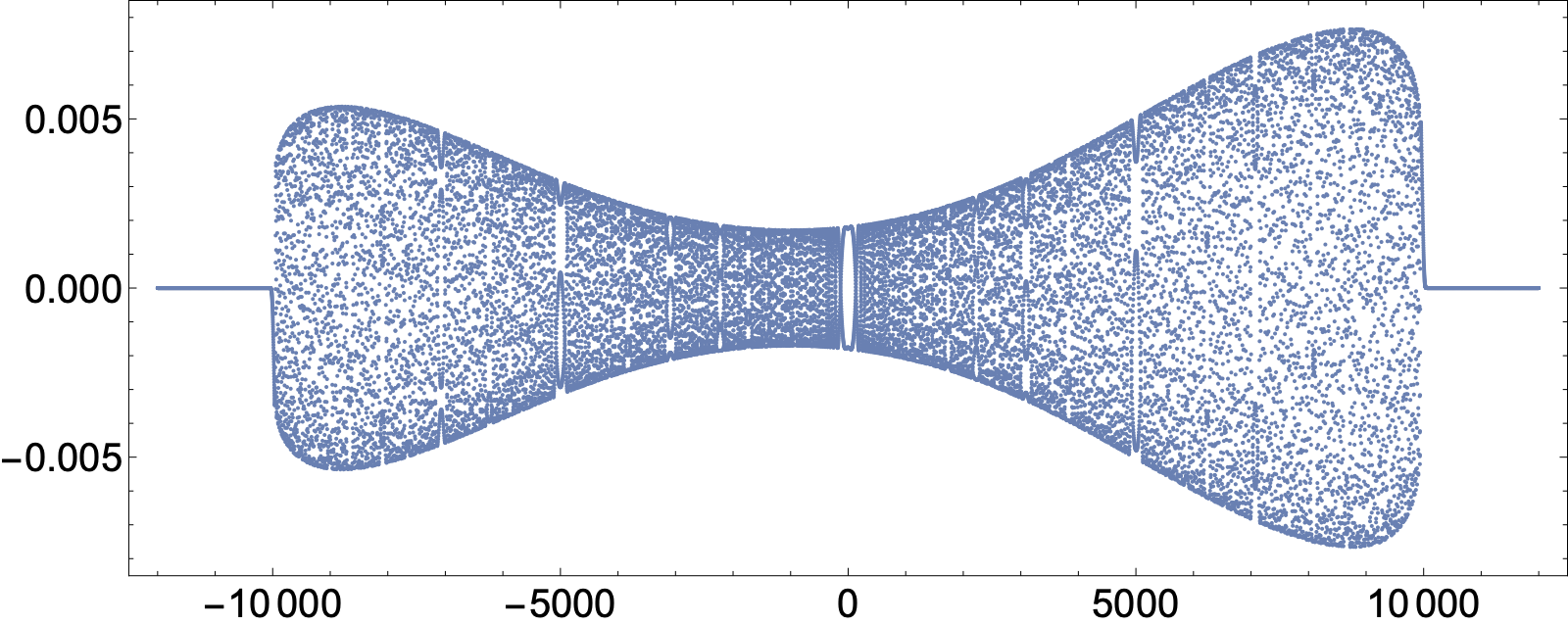
$b_n(t=10000)$, $-7500\leq n\leq 7500$. There are no solitons.
Below is the space-evolution of (truncated) contour for the Riemann-Hilbert problem that’s solved to compute the time evolution of initial data that generates a soliton to $t=1000$. Here $n$ varies from $n=-1250$ to $n=0$.
Numerical contours for the Riemann-Hilbert problem as $n$ varies for fixed $t$.