Efficient computation of soliton gas primitive potentials
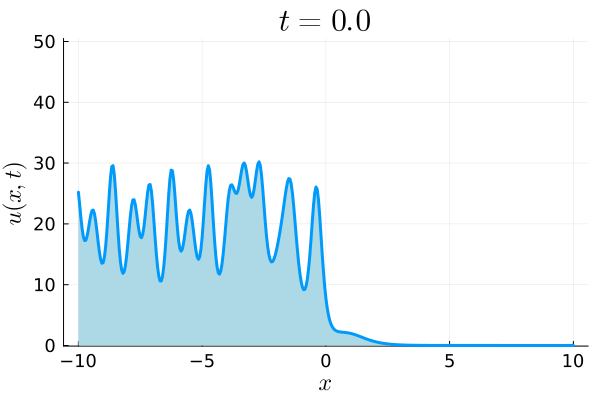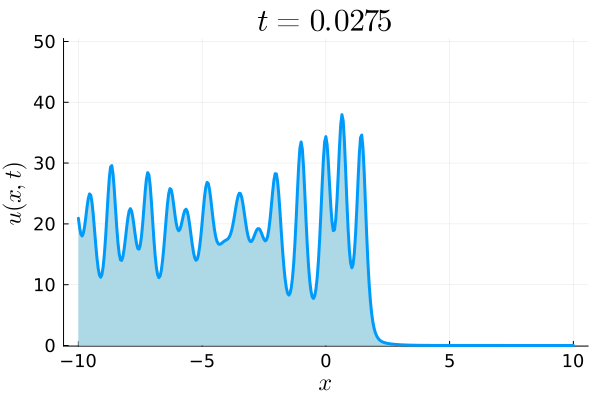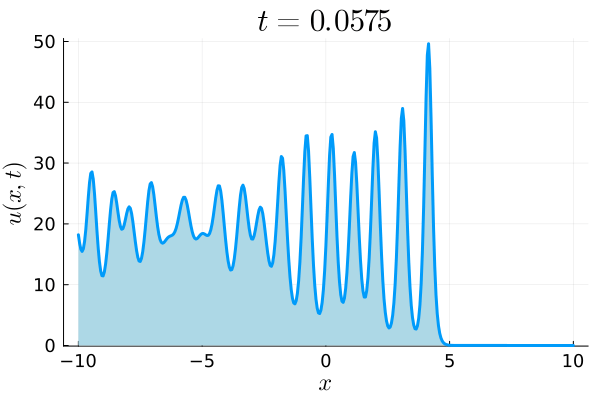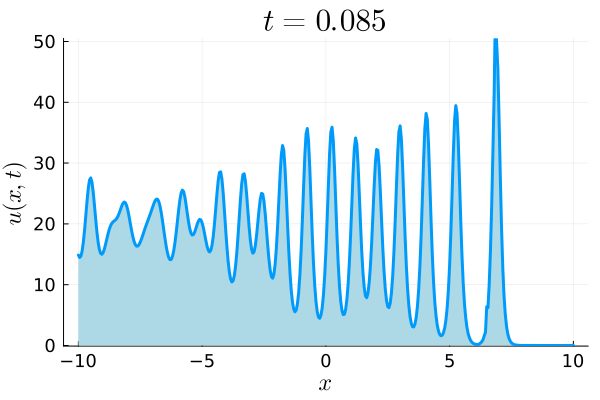 Soliton gas supported on three pairs of bands.
Soliton gas supported on three pairs of bands.
Abstract
We consider the problem of computing a class of soliton gas primitive potentials for the Korteweg-de Vries equation that arise from the accumulation of solitons on an infinite interval in the physical domain, extending to $-\infty$. This accumulation results in an associated Riemann-Hilbert problem on a number of disjoint intervals. In the case where the jump matrices have specific square-root behavior, we describe an efficient and accurate numerical method to solve this Riemann-Hilbert problem and extract the potential. The keys to the method are, first, the deformation of the Riemann-Hilbert problem, making numerical use of the so-called $g$-function, and, second, the incorporation of endpoint singularities into the chosen basis to discretize and solve the associated singular integral equation.
Type
Publication
Journal of Nonlinear Waves 1 e12, 1–19, 2025
This work has also resulted in the software package KdVSolitonGas.jl for Julia.