A Course on Numerical Linear Algebra

Instructor: Deniz Bilman

Textbook: Numerical Linear Algebra, by Trefethen and Bau.

Lecture 3: Norms

We have already used $\| \cdot \|_2$ to denote the Euclidian length. Any function $\| \cdot \| \colon \mathbb{C}^m \to \mathbb{R}$ satisfying

(1) $\|x\| \geq 0$, and $\|x\|=0$ only if $x=0$,

(2) $\|x+y\| \leq\|x\|+\|y\|$ (the triangle inequality),

(3) $\|\alpha x\|=|\alpha|\|x\|$ for any scalar $\alpha\in\mathbb{C}$.

defines a norm on $\mathbb{C}^m$. Some commonly used norms are

$$ \begin{aligned} \|x\|_1 & =\sum_{i=1}^m\left|x_i\right| \\ \|x\|_p & =\left(\sum_{i=1}^m\left|x_i\right|^p\right)^{1 / p} \quad(1 \leq p<\infty)\\ \|x\|_{\infty} & =\max _{1 \leq i \leq m}\left|x_i\right| \end{aligned} $$

using LinearAlgebra
using Plots
using LaTeXStrings

# Define the p-norm function with support for the infinity norm
function p_norm(x1, x2, p)
    if p == Inf
        return max(abs(x1), abs(x2))
    else
        return (abs(x1)^p + abs(x2)^p)^(1/p)
    end
end

# Grid for plotting
x1 = -1.5:0.01:1.5
x2 = -1.5:0.01:1.5

# Values of p to plot
p_values = [ 1, 1.5, 2, 4, Inf]
colors = palette(:tab10)  # Use distinct colors

# Plot the contours
plot(
    aspect_ratio=:equal,
    colorbar=false,
    title="Unit 'disks' in different norms",
    tickfont=font("Computer Modern", 12),
    titlefont=font("Computer Modern", 16),
    legend=:topright  # Ensure legend is positioned at the top-right
)
for (i, p) in enumerate(p_values)
    # Define the label for each p value
    labels = p == Inf ? L"\| x \|_{\infty} = 1" : L"\| x \|_{" * string(p) * "} = 1"
    
    # Add the contour to the plot with the label
    contour!(x1, x2, (x1, x2) -> p_norm(x1, x2, p),
        levels=[1],
        color=colors[i],
        label=labels,
        linewidth=2)
end

# Add labels for axes
xlabel!(L"x_1", guidefont=font("Computer Modern", 16))
ylabel!(L"x_2", guidefont=font("Computer Modern", 16))

Hölder's Inequality

Let $x,y\in\mathbb{C}^m$. We have $$ |x^* y| \leq \|x\|_p \|y\|_q \qquad \text{for}\quad \frac{1}{p}+\frac{1}{q} = 1,\qquad 1\leq p,q \leq \infty. $$

Cauchy-Schwarz Inequality

This is the special case of Hölder's inequality with $p=q=2$: $$ |x^* y| \leq \|x\|_2 \|y\|_2. $$

Matrix Norms Induced by Vector Norms

You should think of it induced norms for a matrix $A\in\mathbb{C}^{m\times n}$ as the norm of the linear mapping $x\in\mathbb{C}^n \mapsto A x \in \mathbb{C}^m$ from $\mathbb{C}^n$ equipped with $\|\cdot \|_p$ to $\mathbb{C}^m$ equipped with $\| \cdot \|_{q}$. Therefore, we define the $(p,q)$ norm of the matrix $A$ as the smallest constant $c>0$ for which the inequality $$ \| A x \|_q \leq c \| x \|_p \qquad \text{for all}\quad x\in\mathbb{C}^n. $$

Therefore, $$ \| A \|_{(p,q)} := \sup _{\substack{x \in \mathbb{C}^n \\ x \neq 0}} \frac{\|A x\|_{q}}{\|x\|_{p}}=\sup _{\substack{x \in \mathbb{C}^n \\\|x\|_{p}=1}}\|A x\|_{q} . $$

It is common practice to work in the setting $p=q$ in many applications. In that case

$$ \| A \|_{p} :=\| A \|_{(p,p)} := \sup _{\substack{x \in \mathbb{C}^n \\ x \neq 0}} \frac{\|A x\|_{p}}{\|x\|_{p}}=\sup _{\substack{x \in \mathbb{C}^n \\\|x\|_{p}=1}}\|A x\|_{p} . $$

Proposition:

For $\displaystyle A\in\mathbb{C}^{m\times n}$, we have $\| A \|_1 = \displaystyle \max_{1\leq j \leq n} \|A_{:,j}\|_1$.

Proof:

Done in class.

Exercise: Similarly, prove the following proposition.

Proposition

The $\infty$-norm $\|A\|_{\infty}$ is equal to the maximum row sum.

Submultiplicativity

For $A\in\mathbb{C}^{m\times n}$ and $B\in\mathbb{C}^{n\times k}$, we have $$ \|A B\|_{(p,q)} \leq \|A\|_{(p,r)}\|B\|_{(r,q)}. $$

Warning: The equality is rarely true. For instance, the inequality $\|A^n\| \leq \|A \|^n$ holds for any square matrix and any matrix norm induced by a vector norm, but the equality $\|A^n\| = \|A \|^n$ does not hold in general for $n\geq 2$.

Theorem:

Any two norms on $\mathbb{C}^m$ are equivalent.

Proof:

Done in class.

A consequence

Theorem:

$\mathbf{C}^m$ equipped with any norm is a complete normed vector space.

Proof:

Done in class.

Theorem:

Let $A\in\mathbb{C}^{m\times m}$ and suppose that there exists a submultiplicative norm $\| \cdot \|$ such that $\| A^p \|<1$ for some power $p\in\mathbb{N}$. Then $\mathbb{I}-A$ is invertible and $$ (\mathbb{I}- A)^{-1} = \sum_{j=0}^{\infty} A^j. $$

Other Norms

Not all matrix norms are induced by a vector norm.

Frobenius Norm (also known as Hilbert-Schmidt Norm)

For $A\in\mathbb{C}^{m\times n}$, $$ \| A \|_{F} := \left(\sum_{i=1}^m \sum_{j=1}^n\left|A_{i j}\right|^2\right)^{1 / 2}. $$ This is the same as the $2$-norm of the vector obtained by viewing $A$ as an $mn$-dimensional vector.

It is an easy exercise to show that the Frobenius norm can also be written in terms of the columns of $A$:

$$ \|A\|_F=\left(\sum_{j=1}^n\left\|A_{:,j}\right\|_2^2\right)^{1 / 2} $$

There is also an analogous result based on the rows of $A$ (just work with $A^\top$). More is true: $$ \|A\|_F= \sqrt{\operatorname{tr}(A^* A)} = \sqrt{\operatorname{tr}(A A^*)} $$ using the trace.

Invariance Under Unitary Multiplication

Proposition:

For any $A \in \mathbb{C}^{m \times n}$ and unitary $Q \in \mathbb{C}^{m \times m}$, we have $\|Q A\|_2=\|A\|_2$ and $\|Q A\|_F=\|A\|_F$.

Proof:

Done in class.

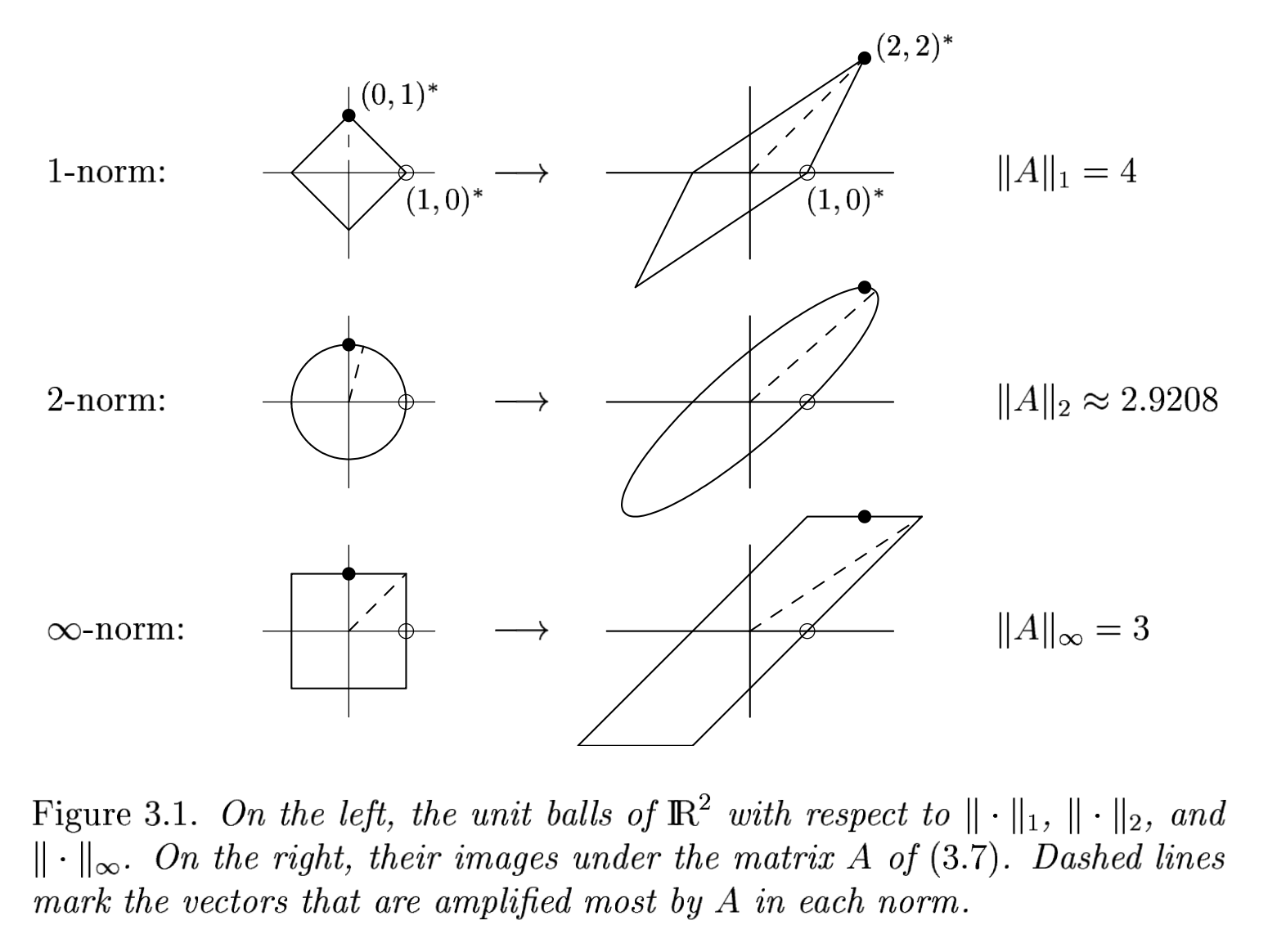
Example

Consider $\displaystyle A= \begin{bmatrix} 1 & 2 \\ 0 & 2\end{bmatrix}$. See the figure below for the effect of $A$ as a transformation from $\mathbb{R}^2$ to $\mathbb{R}^2$.