A Course on Numerical Linear Algebra

Instructor: Deniz Bilman

Textbook: Numerical Linear Algebra, by Trefethen and Bau.

Notational Conventions and Assumptions

All of the matrices and vectors are assumed to be over the field of complex numbers. For instance, when we speak of an $n$ dimensional column vector $x$, we mean $x\in\mathbb{C}^n$. By default, $x\in\mathbb{C}^n$ means that $x$ is a column vector. We use the transpose $x^{\top}$ to denote the row vector. Similarly, $A\in\mathbb{C}^{m\times n}$ means that $A$ is an $m\times n$ matrix. $A_{ij}$ denotes the $(i,j)$ matrix element. We use the "colon" notation meaning "all" and denote the $j$ th column of a matrix $A$ by $A_{:,j}$.

Lecture 1: Matrix-Vector Multiplication

A Matrix Times a Vector

The first order of business is to change our perspective on the multiplication of an $n$-dimensional column vector $x$ and an $m\times n$ matrix $A$.

Writing $b=A x$, burn the bridge to the good old formula giving entries of the vector $b$. Let $A_{:, j}$ denote the $j$ th column of $A$ and observe that $$ b = Ax = \sum_{j=1}^n x_j A_{:,j}. $$ So, $b=Ax$ is the linear combination of the columns of $A$ with coefficients that are the entries of $x$.

Instead of thinking of $Ax=b$ as $A$ acts on $x$ to produce $b$, we are now thinking of $x$ acting on $A$ to produce $b$.

using Random

# Set the random seed
Random.seed!(42)

# Generate a random 4D vector of integers between 1 and 10
x = rand(1:10, 4)
A = rand(1:10, (4,4))

4×4 Matrix{Int64}:
 7  5  4  3
 2  3  3  2
 7  7  6  5
 7  7  1  5

A*x

4-element Vector{Int64}:
 118
  60
 154
 129

A[:,1]*x[1]+A[:,2]*x[2]+A[:,3]*x[3]+A[:,4]*x[4]

4-element Vector{Int64}:
 118
  60
 154
 129

A Matrix Times a Matrix

This perspective extends to multiplication of a matrix by another matrix. We know that if $A$ is $\ell \times m$ and $C$ is $m \times n$, then $B$ is $\ell \times n$, with entries defined by $$ B_{ij} = \sum_{k=1}^{m} A_{i k} C_{k j}. $$ Again, we interpret this good old formula in terms of columns. The $j$th column of the matrix $B$ is a linear combination of the columns of $A$ with coefficients given by the $j$ th column of $C$: $C_{:, j}$. Therefore, $$ B_{:,j} = A C_{:,j} = \sum_{k=1}^m C_{kj} A_{:,k} $$

Special Example: Outer Product

The outer product is phrased as a special product of two vectors $u\in\mathbb{C}^m$ and $v\in\mathbb{C}^n$. Their outer product is the $m\times n$ matrix $u v^{\top}$: $$ (u v^{\top})_{i j} = u_i v_k. $$ Thinking of this as a matrix times a matrix, we can wire this product formula in terms of columns. Then $$ (u v^{\top})_{:,j} = v_j u. $$ As you see, the $j$ th column of the outer product $u v^{\top}$ is $v_j$ times the column vector $u$. This easily shows that $u v^{\top}$ is a rank-1 matrix.

u = [ 1; 2im; 3 ];  # column vector
v = [ 2 -1 1 ]; #row vector
size(u)|>display
size(v)|>display
u*v

(3,)

(1, 3)

3×3 Matrix{Complex{Int64}}:
 2+0im  -1+0im  1+0im
 0+4im   0-2im  0+2im
 6+0im  -3+0im  3+0im

Range and Nullspace

Range

The range of matrix $A\in\mathbb{C}^{m\times n}$ is denoted by $\operatorname{range}(A)$ and it is the set of vectors that can be written as $A x$ for some $x$. Form our point of view of the matrix-vector product, it is clear that $\operatorname{range}(A)$ is the space spanned by the columns of $A$.

Range of $A$ is sometimes called the columnspace of $A$.

Nullspace

The nullspace of $A\in\mathbb{C}^{m\times n}$ is denoted by $\operatorname{null}(A)$ and it is the set of vectors $x$ satisfying $Ax=0$. You may think of this as the space spanned by vectors that are annihilated (or "killed") by $A$. From our perspective, a vector $x\in \operatorname{null}(A)$ gives the coefficients of an expansion of zero as a linear combination of the columns of $A$:

$$ 0 = x_1 A_{:,1} + x_2 A_{:,2} + \cdots + x_n A_{:,n}. $$

Rank

The column rank of $A$ is the dimension of its columnspace. So, by definition, the column rank is $\dim(\operatorname{range}(A))$.

The row rank of $A$ is the dimension of its rowspace (the space spanned by the rows of $A$).

Fundamental fact: Row rank always equals column rank.

So we refer to this number simply as the rank of a matrix.

An $m\times n$ matrix of full rank is one that has the maximal possible rank (the lesser of $m$ and $n$). This means that a matrix of full rank with $m \geq n$ must have $n$ linearly independent columns. Such a matrix can also be characterized by the property that the map it defines is one-to-one.

Theorem

A matrix $A \in \mathbb{C}^{m \times n}$ with $m \geq n$ has full rank if and only if it maps no two distinct vectors to the same vector.

Proof of the Theorem

Done in class.

using LinearAlgebra
A = [ 0 1; 0 0 ]
rank(A)

1

B = [ 1 4;  2 8 ]
rank(B)

1

With finite precision arithmetic of computers relying on a numerically computed rank of a matrix is not a good idea.

Inverse

A nonsingular or invertible matrix is a square matrix of full rank. Note that the $m$ columns of a nonsingular $m \times m$ matrix $A$ form a basis for the whole space $\mathbb{C}^m$.

# Perturbing the second row of A by a very tiny amount yields and invertible matrix:

rank(A + [ 0 0; 1e-14 0])

2

Since the columns of an invertible matrix $A$ form a basis for $\mathbb{C}^m$, any vector in $\mathbb{C}^m$ can be expressed as a unique linear combination of the columns of A. In particular, the canonical unit vectors $\mathbf{e}_j\in\mathbb{C}^m$ (1 at the $j$th spot and zeros elsewhere):

$$ \mathbf{e}_j = \sum_{i=1}^{m} z_{i j} A_{:,i} $$

for some scalars $z_{ij}$. Let $Z$ be the matrix with entries $z_{i j}$. Then

$$ \mathbb{I} = A Z. $$

The matrix $Z$ is the inverse of $A$.

Any square nonsingular matrix $A$ has a unique inverse, written $A^{-1}$, that satisfies $A A^{-1}=A^{-1} A=I$.

Theorem

For $A \in \mathbb{C}^{m \times m}$, the following conditions are equivalent:

(a) A has an inverse $A^{-1}$,

(b) $\operatorname{rank}(A)=m$,

(c) $\operatorname{range}(A)=\mathbb{C}^m$,

(d) $\operatorname{null}(A)=\{0\}$,

(e) 0 is not an eigenvalue of $A$,

(f) 0 is not a singular value of $A$,

(g) $\operatorname{det}(A) \neq 0$.

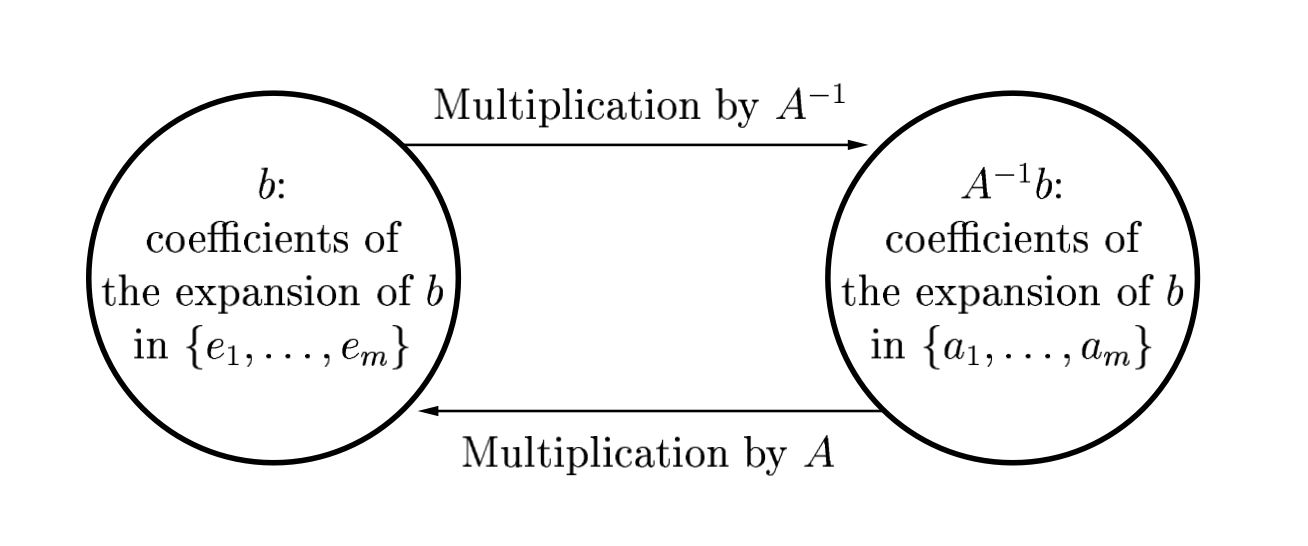
A Matrix Inverse Times a Vector (Change of Basis)

When we write

$$ x=A^{-1} b $$

we should think of $x$ as the unique vector that satisfies the equation $A x = b$. This means the following:

$A^{-1} b$ is the vector of coefficients of the expansion of $b$ in the basis of columns of $A$.

So multiplication by $A^{-1}$ is a change of basis operation:

# Generate a random 3x3 matrix integers between 1 and 10
Random.seed!(42)
x = [-1; 2; -1]
A = rand(1:10, (3,3))
rank(A)|>display
b = A*x
# b=Ax is the coefficients of the expansion of b in the standard basis so we define
b_coeffs_standard = A*x |>display
# A^{-1} b is the coefficients of the expansion of b in the basis of columns of A.
b_coeffs_colA = A^(-1) * b |>display

3

3-element Vector{Int64}:
  2
  2
 -6

3-element Vector{Float64}:
 -0.9999999999999997
  2.0
 -1.0000000000000002

For reasons to be explained later, never compute the inverse of a matrix numerically. Instead do A \ b:

b_coeffs_colA = round.(A \ b)

3-element Vector{Float64}:
 -1.0
  2.0
 -1.0