Long-time asymptotics for Hamiltonian perturbations of the Toda lattice

This website is devoted to a project investigating long-time asymptotics for Hamiltonian perturbations of the (completely-integrable) doubly-infinite Toda lattice.

Below we present computational results which complement the paper

by:

Deniz Bilman, University of Illinois at Chicago
Irina Nenciu, University of Illinois at Chicago

Hamiltonian Perturbations of the Toda Lattice

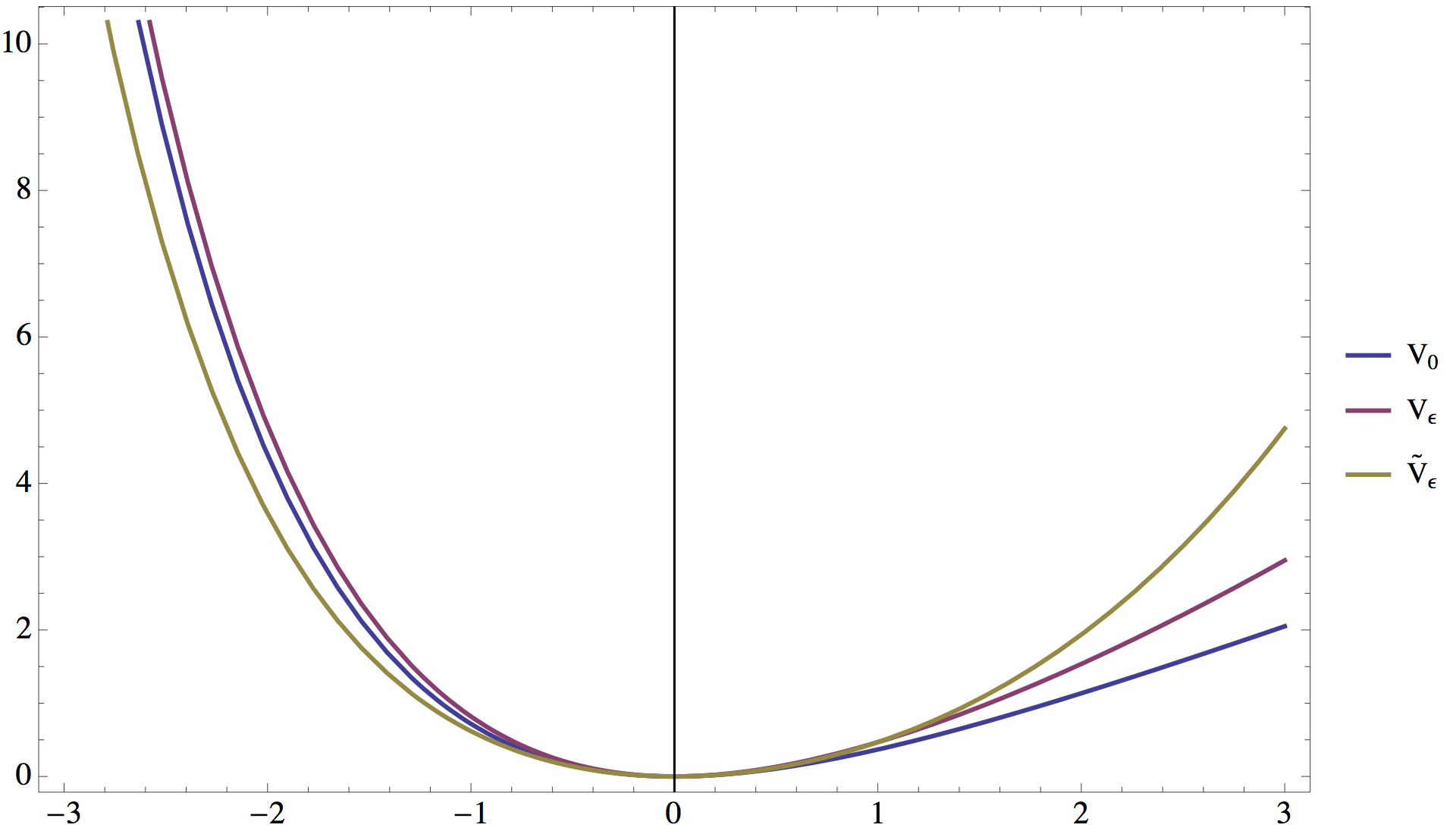
We study of perturbations of the doubly-infinite Toda lattice induced by perturbed interaction potentials of the form: $$ V_\varepsilon(r) = V_0(r) + \varepsilon u(r)\, ,$$where $V_0(r) = e^{-r} + r - 1$ is the Toda potential. Here $\varepsilon > 0$ is small and $u$ is fixed a perturbation function chosen so that the resulting system is globally well-posed in time and possesses solitary wave solutions.

In the Flaschka variables, $(a,b)$, the equations of motion are given by \begin{equation} \begin{cases} \partial_t{a}_n = a_n\big(b_{n+1} - b_n\big)\\ \partial_t{b}_n = 2\big(a_n^2 - a_{n-1}^2\big) + \frac{\varepsilon}{2} \big( u'\big(c_{n-1}\big) - u'\big(c_n \big)\big)\, \end{cases} \end{equation} where \begin{equation}\label{E:defn_c} c_n = \log{\left(\frac{1}{4a_n^2}\right)}\,, \end{equation} for all $n\in \mathbb{Z}$. The system above can be recasted as a perturbation of the isospectral evolution on Jacobi matrices: \begin{equation} \partial_t{L} = [P, L] + \varepsilon U\,, \end{equation} where \begin{equation} L= \begin{pmatrix} \ddots &\ddots & \ddots & \\ \ddots & b_{n-1} & a_{n-1} & 0 \\ \ddots & a_{n-1} & b_n & a_n & \ddots \\ & 0 & a_n & b_{n+1} & \ddots \\ & & \ddots &\ddots & \ddots \\ \end{pmatrix} %\end{equation*} \qquad\text{and}\qquad %\begin{equation*} P= \begin{pmatrix} \ddots &\ddots & \ddots & \\ \ddots & 0 & a_{n-1} & 0 \\ \ddots & -a_{n-1} & 0 & a_n & \ddots \\ & 0 & -a_n &0 & \ddots \\ & & \ddots &\ddots & \ddots \\ \end{pmatrix}\,, \end{equation} and $U$ is a diagonal matrix with \begin{equation} U_{nn} =\frac{1}{2} \big( u'\big(c_{n-1}\big) - u'\big(c_n \big)\big)\,. \end{equation}

We consider solutions $(a,b)$ which satisfies \begin{equation} \sum_{n\in\mathbb{Z}}(1+| n |)\Big(\big|2 a_n - 1\big| + \big|b_n\big|\Big) < \infty\,. \end{equation} This implies that the discrete spectrum of $L$ consists of finitely many real simple eigenvalues, and $\sigma_{\textrm{ess}}(L)=[-1,1]$ is absolutely continuous.

Some plots and animations

A pure 1-soliton solution of the Toda lattice is evolving under perturbations $u(r) = r^2$ (the movie in the top pane) and $u(r)=r^3$ (the movie in the bottom pane), with $\varepsilon=0.05$ from time $t=0$ to $t=100$. The Toda soliton ($\varepsilon=0$) is plotted in blue and the solutions under the perturbed dynamics are plotted in red and purple. The animation is also available in full-screen mode.

Below, the same pure 1-soliton solution of the Toda lattice is evolving under perturbations $u(r) = 1 - \cos r$ (the movie in the top pane) and $u(r)=r^2 + r^3$ (the movie in the bottom pane), with $\varepsilon=0.05$ from time $t=0$ to $t=100$. The Toda soliton ($\varepsilon=0$) is again plotted in blue and the solutions under the perturbed dynamics are plotted in red and purple. The animation is also available in full-screen mode.

Below is a taller pure 1-soliton solution of the Toda lattice is evolving under perturbation $u(r) = r^2$, with $\varepsilon=0.05$ from time $t=0$ to $t=80$. The Toda soliton ($\varepsilon=0$) is again plotted in blue and the solution under the perturbed dynamics is plotted in red. The animation is also available in full-screen mode.

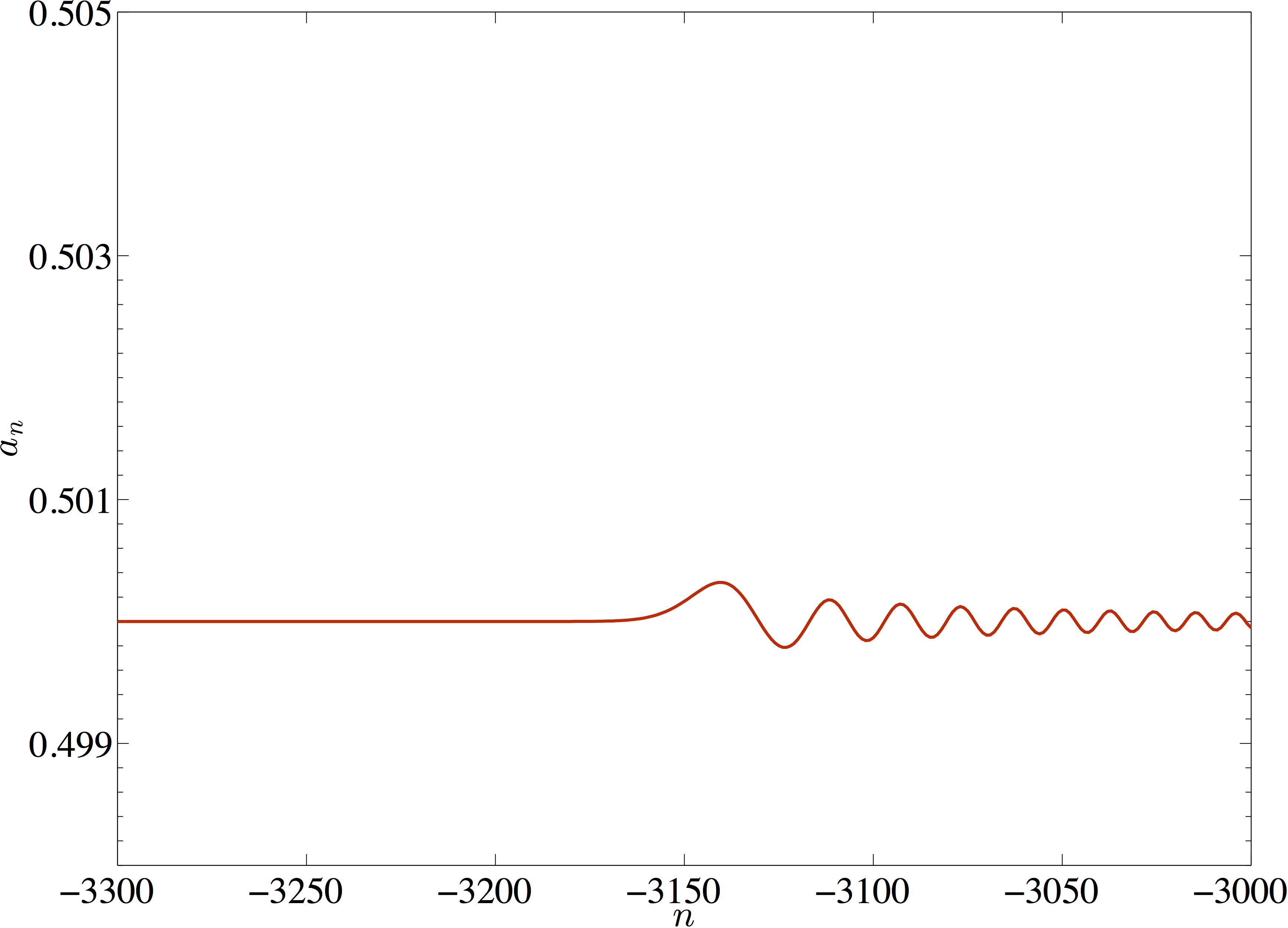
In the following two plots, the top part of the wave is truncated to show the details of the dispersion.

Solitary wave solution of the lattice with $u(r)=r^2$ and $\varepsilon = 0.05$, followed by a dispersive tail.

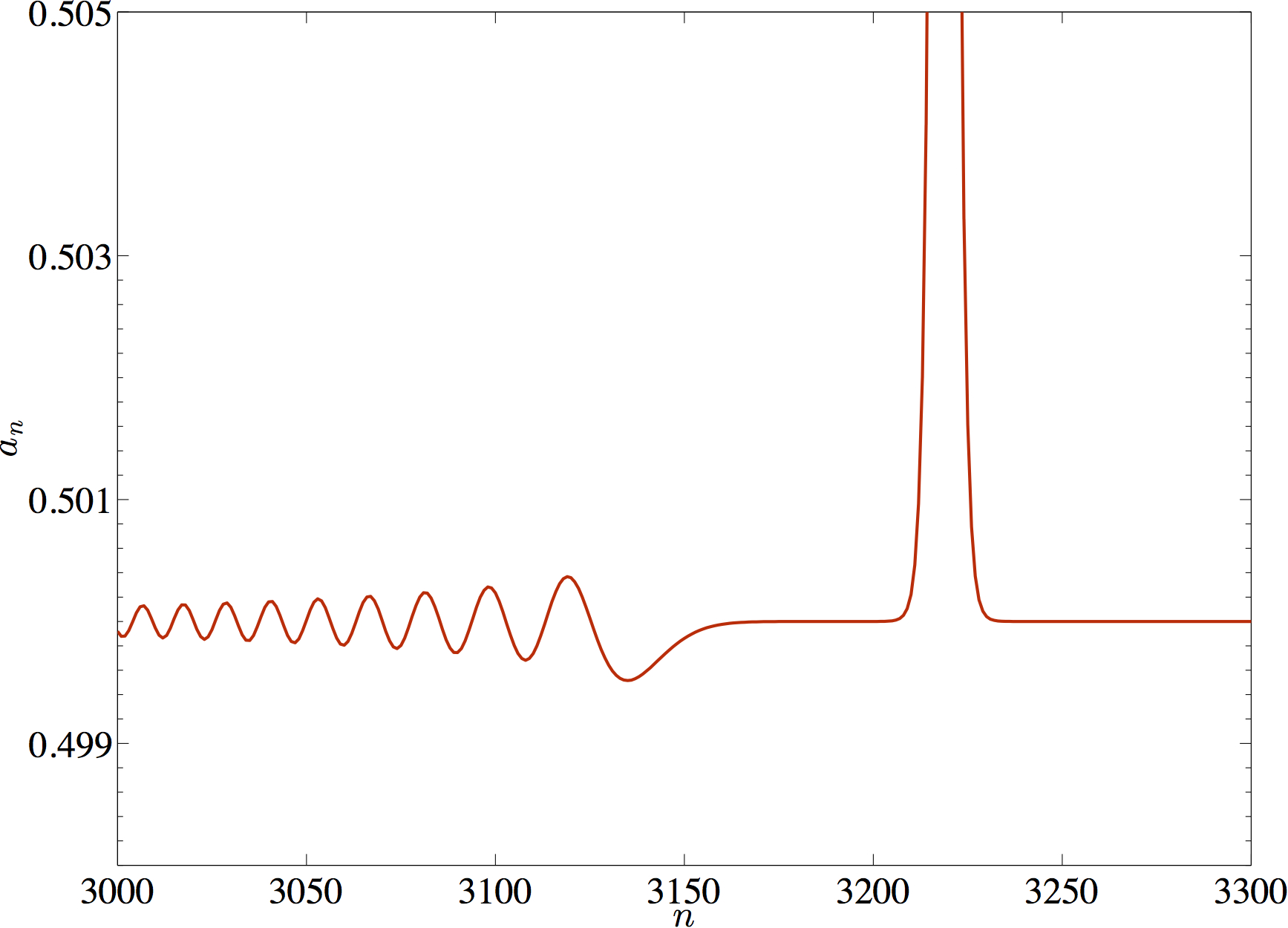
Counter propagating dispersive wave in the lattice with $u(r)=r^2$ and $\varepsilon = 0.05$.

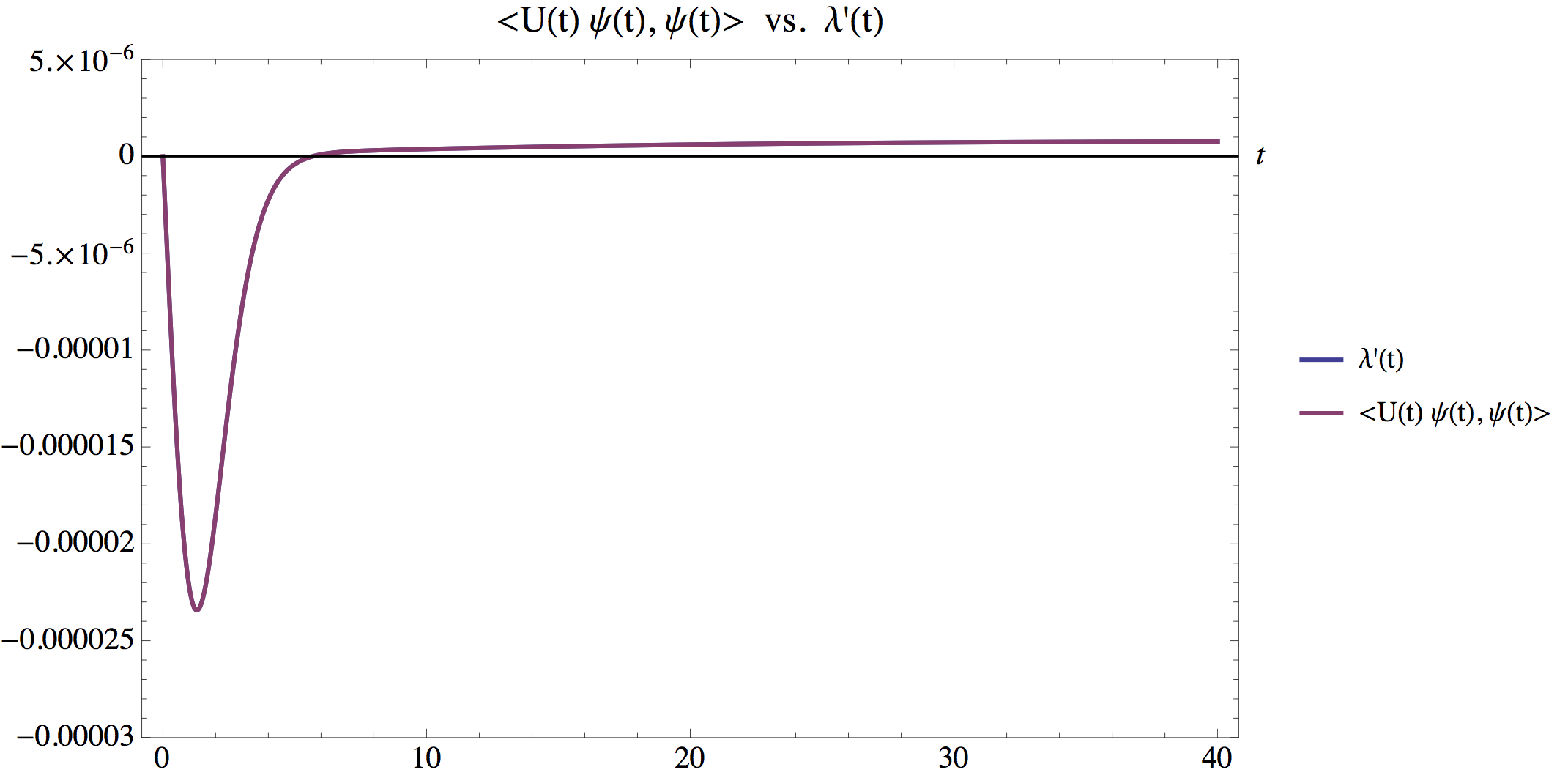
The plot below compares the right hand side of $\partial_t\lambda = \varepsilon\langle U \psi, \psi \rangle$ with $\partial_t\lambda$ obtained through the computed scattering data for the lattice with $u(r)=r^2$ and $\varepsilon = 0.05$, in a small time scale; and $\psi$ is the associated normalized eigenvector. We note that $\partial_t \lambda \sim 0$ for long time scales.

Below, 2 equal sized clean solitary wave solutions of the perturbed lattice with $u(r) = r^2$ and $\varepsilon=0.05$ are interacting in a head-on collision. The animation is also available in full-screen mode.

Absolute value of the reflection coefficient $|R(z;t)|$ associated with a clean solitary wave solution of the lattice with $u(r)=r^2$ and $\varepsilon = 0.05$, evolving from time $t=0$ to $t=100$.

A new eigenvalue emerging from bottom of the ac spectrum in the lattice with $u(r)=r^2$ and $\varepsilon = 0.05$. The initial data used in this simulation is a purely dispersive solution of the Toda lattice, i.e. one for which $\sigma_{d}(L) = \varnothing$ at $t=0$.

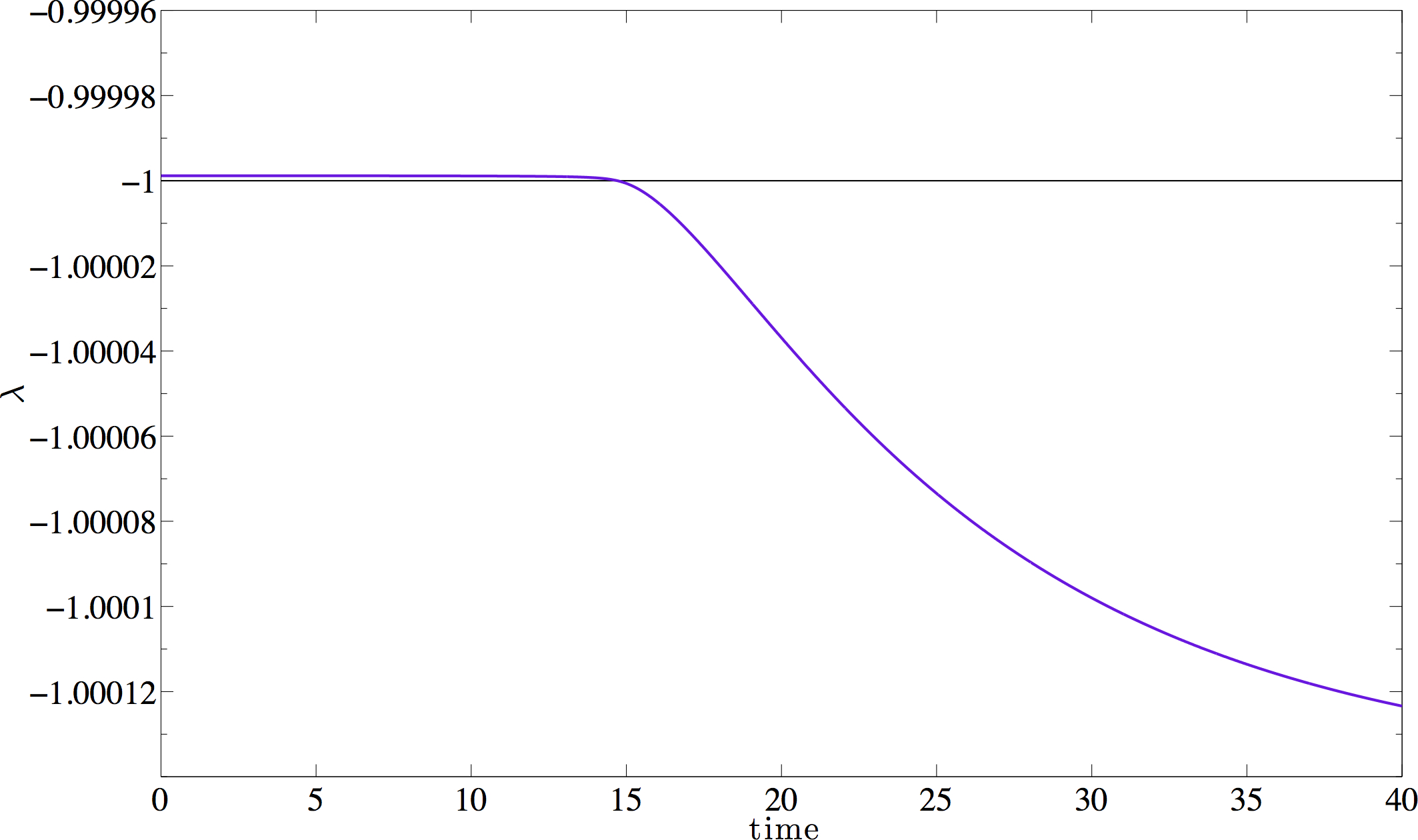
Below is the corresponding solution from time $t=0$ to $t=40$ in a lattice with $N=4096$ particles. $(a_n)_n$ is plotted in blue and $(b_n)$ is plotted in red.

This is the same animation, but the particles are not joined by curves.